Names of angles:
In this lesson let me help you on acute angle. An angle is the formed by two rays sharing a common endpoint, called the vertex of the angle. The magnitude of the angle is the "amount of rotation" that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other (“Measuring angles").
Name of Angles Types:
1) Acute angle.
2) Right angle.
3) Obtuse angle.
4) Straight angle.
5) Reflex angle.
6) Adjacent angles.
7) Vertical angles.
8) Complementary angles.
This could also help us on factor by grouping.
Acute Angle:
An acute angle is any angle whose measure is less than 90 degree.
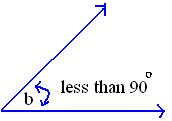
I hope this exaplanation is very easy for you to understand. Keep reading may be in the next session let me help you on Fractions Calculator
In this lesson let me help you on acute angle. An angle is the formed by two rays sharing a common endpoint, called the vertex of the angle. The magnitude of the angle is the "amount of rotation" that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other (“Measuring angles").
Name of Angles Types:
1) Acute angle.
2) Right angle.
3) Obtuse angle.
4) Straight angle.
5) Reflex angle.
6) Adjacent angles.
7) Vertical angles.
8) Complementary angles.
This could also help us on factor by grouping.
Acute Angle:
An acute angle is any angle whose measure is less than 90 degree.

I hope this exaplanation is very easy for you to understand. Keep reading may be in the next session let me help you on Fractions Calculator
